Стоковые векторные изображения по запросу Геометрические фигуры
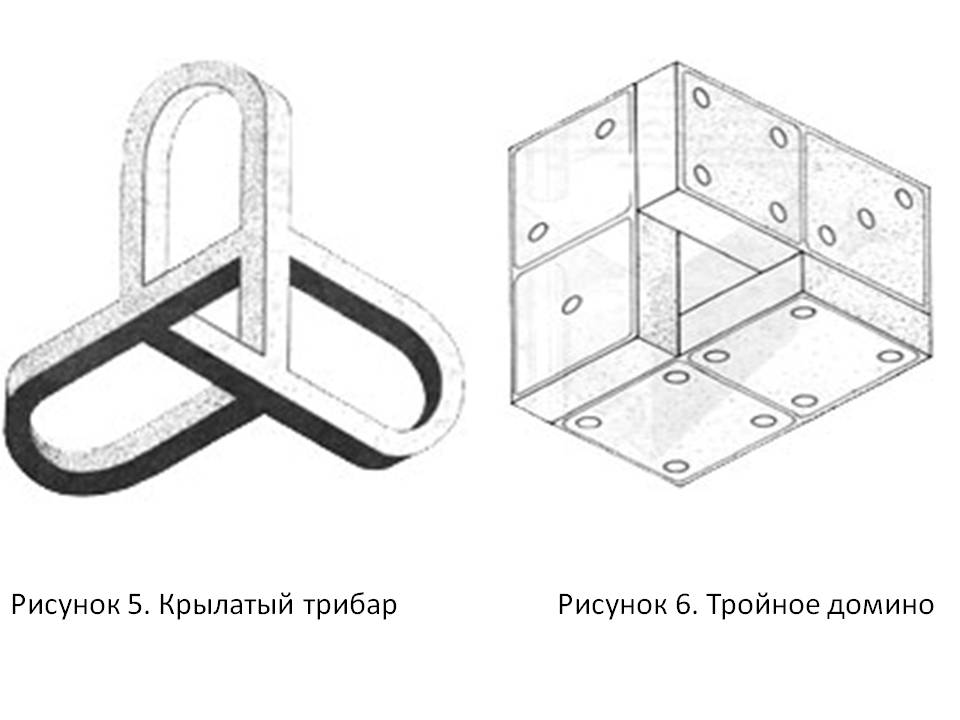
Она появилась в году в журнале British Journal of Psychology, в статье под заголовком "Удивительные фигуры, особый вид оптических иллюзий". Ее авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как "трехмерную прямоугольную структуру". Она также получила название "трибар", или "деформированный трибар". В этой статье фигурировали еще два загадочных объекта. Таким образом, "невозможные объекты" были впервые представлены широкой общественности на примере этих трех фигур. Вскоре Мауриц К.




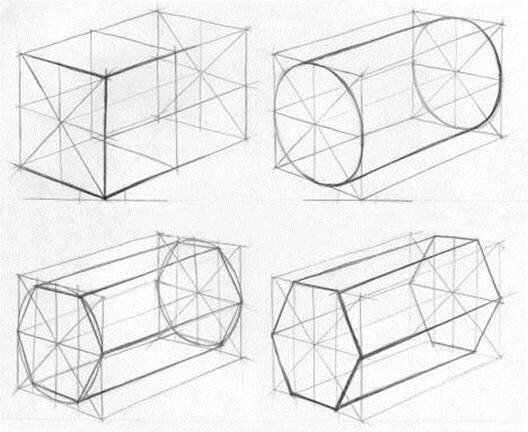
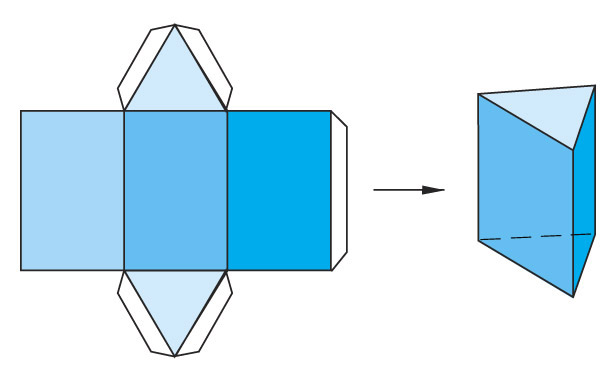


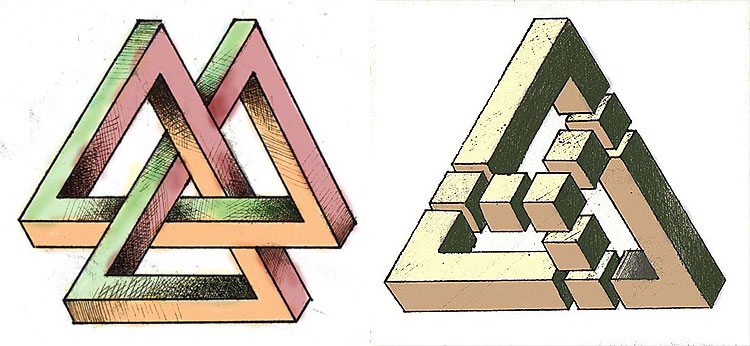
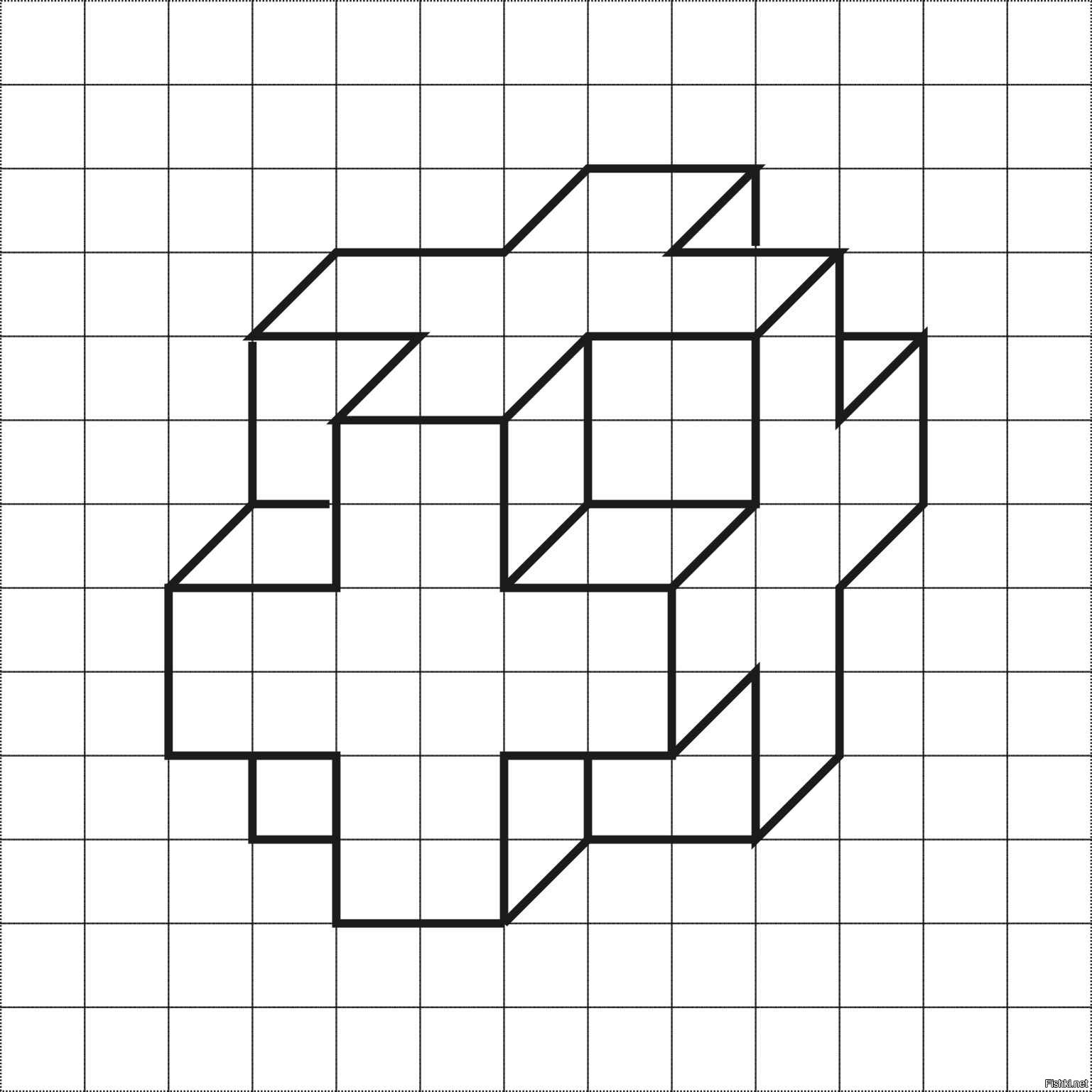
Скорее всего, это будут мысли о треугольниках и квадратах, круге и ромбе. Предлагаем познакомить малышей с этим увлекательным миром и предложить им интересные геометрические головоломки! Эти занимательные задачки подойдут и дошкольникам, и детям постарше и раскрасят череду повседневных игр. Геометрические головоломки развивают абстрактное и логическое мышление, воображение, комбинаторные способности, а также терпение и усидчивость, ведь составление новых фигур требует времени. Мы подобрали для вас 25 занимательных задач по геометрии и уверены, что их решение принесёт не только пользу, но и большое удовольствие вашему ребёнку. Посмотрите, сколько треугольников на этом рисунке?
- Îñêàð Ðåóòåðñâàðä: èçîáðåòàòåëü íåâîçìîæíûõ ôèãóð
- Гипотеза проекта: в мире существуют необычные геометрические фигуры, которые невозможно объяснить с точки зрения традиционной геометрии Задачи проекта : рассмотреть необычные треугольники, квадрат, кривые и необычные предметы Цель проекта: изучить необычные геометрические фигуры. Необычные треугольники Оказывается, в нашем мире существуют треугольники, которые совсем не похожи на те треугольники, которые м все знаем с детства.
- Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
- Изобразить фигуру в 4 измерении просто невозможно и на это есть 2 причины: 1. Наши глаза не видят даже трёхмерность если захотите по подробнее узнать об этом, то пишите в комментах, а я постараюсь в следующей статье вам это объяснить.
- Выполните развивающие упражнения от Айкьюши
- Ознакомление детей дошкольного возраста с геометрическими фигурами имеет большую ценность для развития их познавательного интереса.
- Какие фигуры ты знаешь?
- На уроках геометрии мы часто сталкиваемся с такой проблемой: рассматривая свойства геометрических фигур, некоторые ученики иногда опираются лишь на чертеж, на свое зрительное восприятие. Но такой подход к решению задачи часто приводит к ошибочным выводам, а значит к неверному решению.













| 356 | Показано 59 страниц из 59, находящихся в данной категории. | |
| 491 | Волчкевич г. Аннотация: Данный материал представляет собой второй параграф курса геометрии 7 класса для школ участников проекта "Математическая вертикаль". | |
| 72 | На моём канале недавно была статья про простые геометрические фигуры в разных измерениях. | |
| 463 | Еще в году американский психолог, доктор наук Сьюзен Деллингер создала уникальную систему типирования личности. Она назвала ее психогеометрией и показала, как выбор геометрической фигуры, которая нравится больше всего, очень метко раскрывает характер человека. | |
| 432 | Отправить комментарий. | |
| 22 | Скорее всего, это будут мысли о треугольниках и квадратах, круге и ромбе. Предлагаем познакомить малышей с этим увлекательным миром и предложить им интересные геометрические головоломки! | |
| 441 | Мы привыкли доверять собственному зрению, однако оно нередко обманывает нас, показывая то, чего в действительности не существует. В такие моменты мы сталкиваемся со зрительными иллюзиями — ошибками зрительного восприятия. |
Невозможная фигура — один из видов оптических иллюзий , фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. Создаётся иллюзия невозможности существования такой фигуры в трёхмерном пространстве. На самом деле все невозможные фигуры могут существовать в реальном мире.